University of Sydney, Australia

ReDro: Efficiently Learning Large-sized
SPD Visual Representation


Saimunur Rahman1,2, Lei Wang1, Changming Sun2 and Luping Zhou3


1   University of Wollongong, Australia            2   CSIRO Data61            3   University of Sydney, Australia


[Paper]                      [Code]                      [BibTex]



University of Sydney, Australia


Abstract

Symmetric positive definite (SPD) matrix has recently been used as an effective visual representation. When learning this representa- tion in deep networks, eigen-decomposition of covariance matrix is usu- ally needed for a key step called matrix normalisation. This could result in significant computational cost, especially when facing the increasing number of channels in recent advanced deep networks.
This work proposes a novel scheme called Relation Dropout (ReDro). It is inspired by the fact that eigen-decomposition of a block diagonal matrix can be efficiently obtained by decomposing each of its diagonal square matrices, which are of smaller sizes. Instead of using a full co- variance matrix as in the literature, we generate a block diagonal one by randomly grouping the channels and only considering the covariance within the same group. We insert ReDro as an additional layer before the step of matrix normalisation and make its random grouping transparent to all subsequent layers. Additionally, we can view the ReDro scheme as a dropout-like regularisation, which drops the channel relationship across groups. As experimentally demonstrated, for the SPD methods typically involving the matrix normalisation step, ReDro can effectively help them reduce computational cost in learning large-sized SPD visual representation and also help to improve image recognition performance.



Key Results

     



Supplementary Information

Supplementary Copy

Short Video (<=1 min.)

Long Video (<=10 min.)




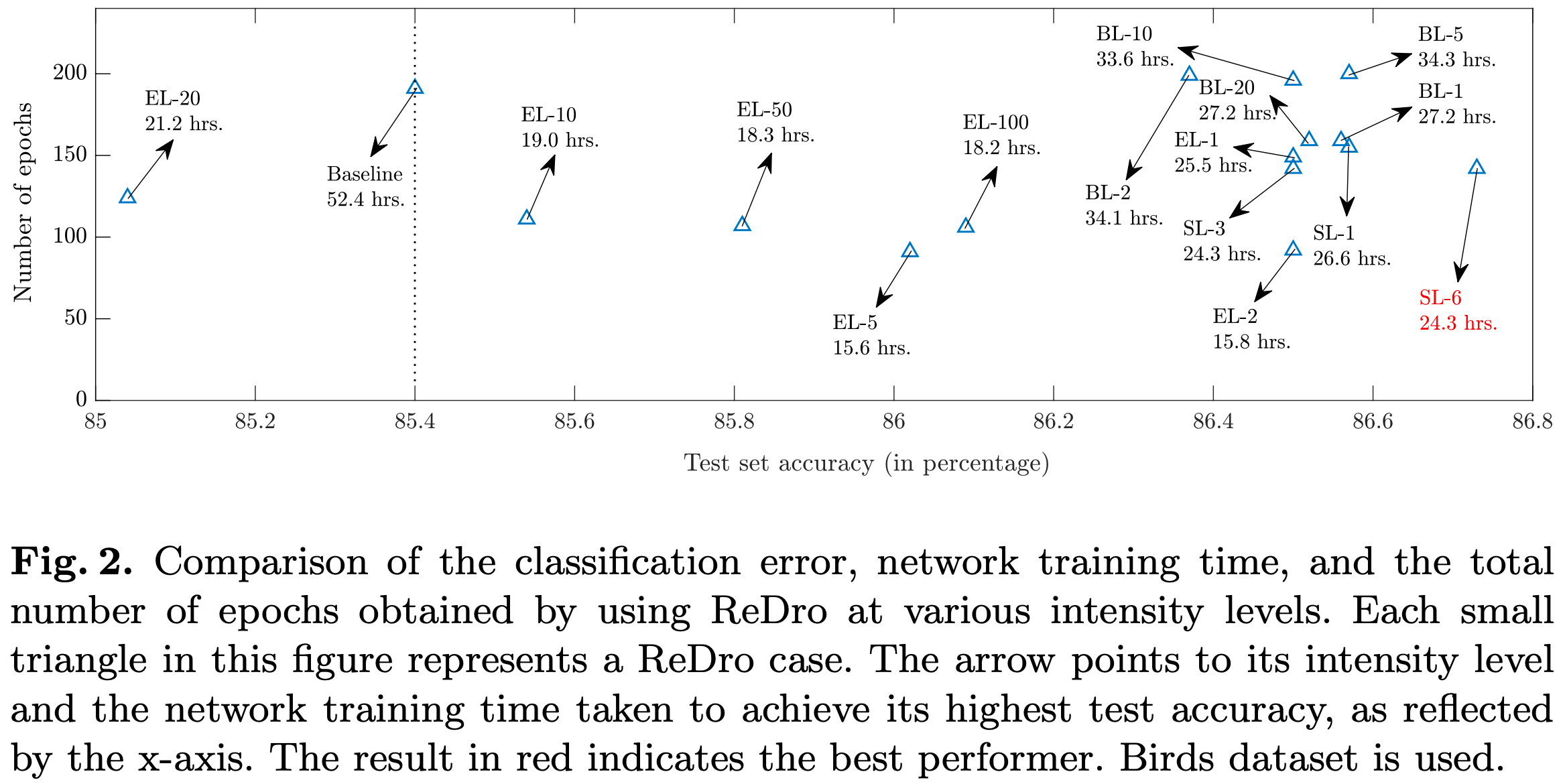
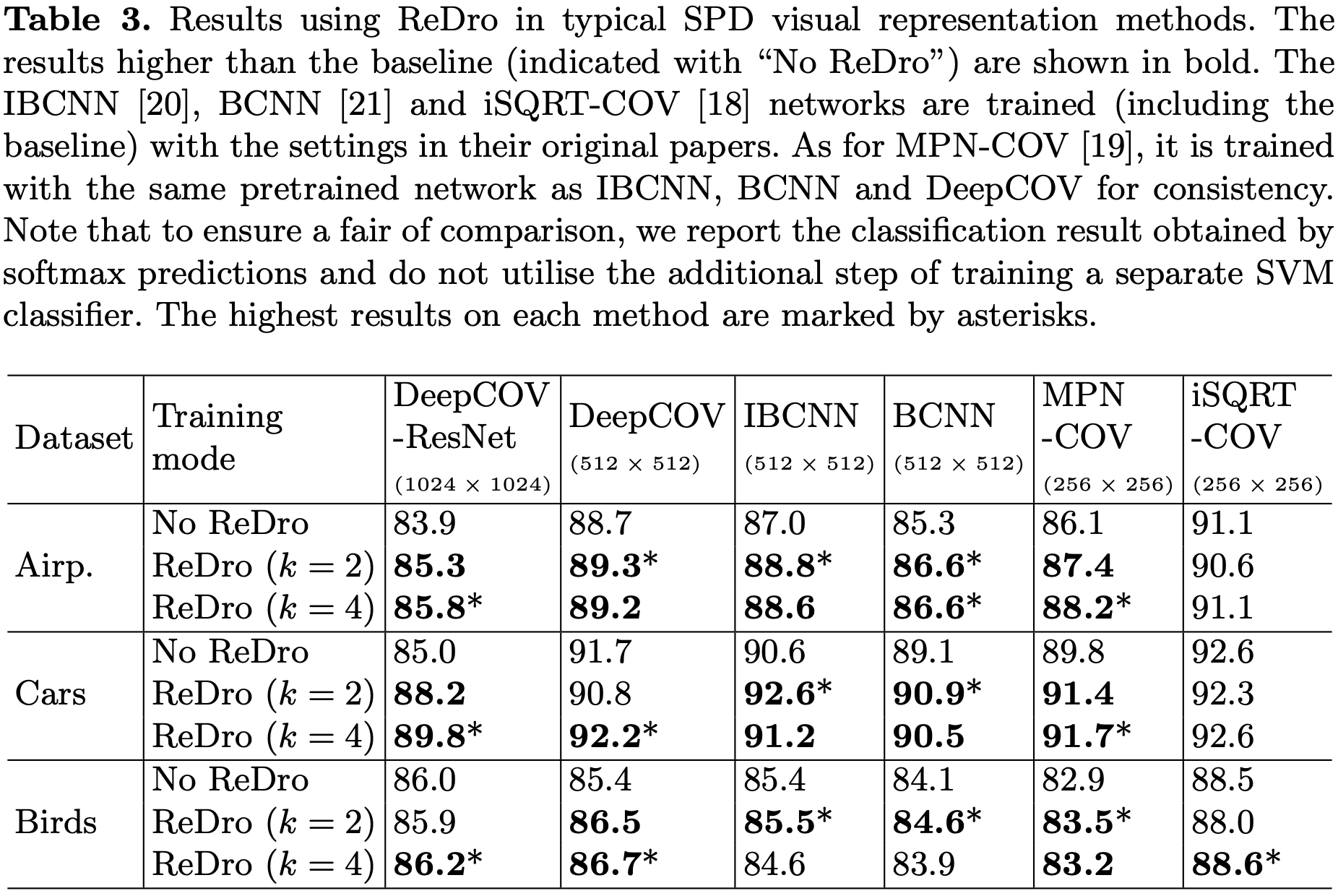
Acknowlegements

Funding for this research is provided by the Commonwealth Scientific and Industrial Research Organisation (CSIRO) and University of Wollongong, Australia. LZ is funded by the Australian Research Council (grant number DP200101289). SR is supported through CSIRO Data61 PhD Scholarships. Support also received from Multi-modal Australian ScienceS Imaging and Visualisation Environment (MASSIVE).